최근 프로젝트를 완료하면서, 개인적으로 다시 한번 파이썬(Python)에 대한 정리 필요성을 느끼게 되어 해당내용을 하나씩 기록하고자 합니다.
프로그래밍 언어를 공부시 개인적으로 제일 먼저 친해져야 하는 명령어가 출력문이다. 그 이유는 당연히 백문이 불여일견이 듯이, 백문이 불여일타의 첫시작이 출력문이기 때문이다.
# 문자열(string) 출력
print('Maing M&F')
# 문자열 포매팅(string formatting): 문자열의 원하는 위치에 변수값을 출력하는 것을 의미함
# 1) % 사용(서식문자): 정수(%d), 문자열(%s), 실수(%f), 문자(%%)...
str_sample1 = 'Hello %s' % 'Python'
print(str_sample1)
str_sample2 = 'My age: %d' % 18
print(str_sample2)
number = 1004
str_sample2 = 'My happy nummber : %d' % number
gifts=['bag','money','travel']
for gitf in gifts:
print('My gift is %s' % gitf)
# 인자가 두개 이상인경우: ()를 사용
str_sample3 = 'my name is %s and age is %d' % ('M&F',18)
print(str_sample3)
## 단점: formatter에 대응되는 데이터 타입을 정확히 알아야 하고,
## 코드가 길어지면 가독성이 떨어짐
# 2) str.format 사용(Python 3이상 부터 지원)
str_sample4 = 'Python version {}'.format(3)
print(str_sample4)
str_sample5 = 'My name: {}'.format('wonwoo')
print(str_sample5)
# multiple arguments
str_sample6 = 'My name is {0} and my age is {1}'.format('wonwoo',18)
print(str_sample6)
## 단점: 긴 문자열 처리 및 여러인자 일때 너무 문자열 길이가 길어지는 느낌!
# 3) f-string(Python 3.6이상 부터 지원)
name = 'wonwoo'
str_sample7 = f'My name is {name}'
print(str_sample7)
age = 18
str_sample8 = f'My name is {name} and age is {age}'
print(str_sample8)
## 정리: f-string이 가장 직관적이다. 사용하기 쉽다. 또한 속도 면에서도 가장빠르다.

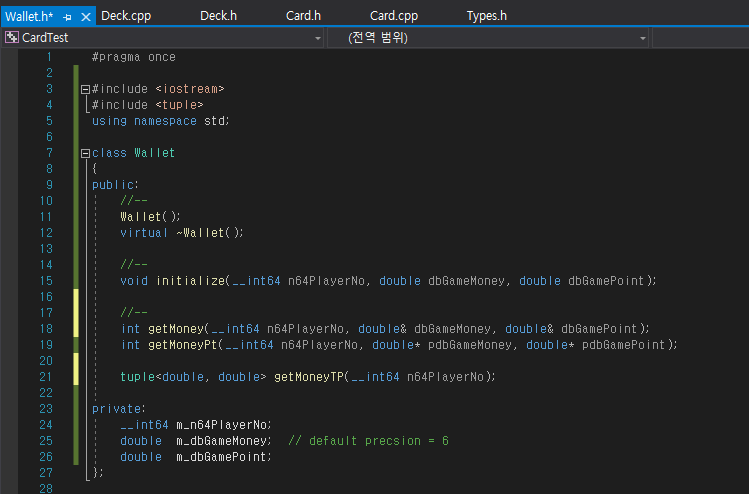
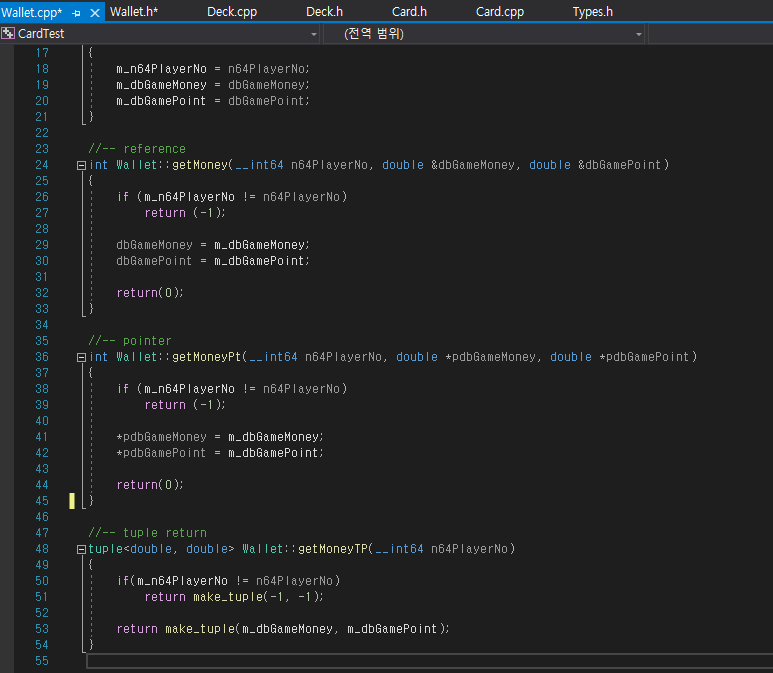
C/C++개발 경험 관점에서, Python으로 작업을 하게 되면 제일 좋게 느껴지는 점은 자료구조(set, list, tuple 등)의 직관성입니다. (물론, C++ 에서도 지원을 하고 있지만, 상대적으로 익숙해지는 시간이 조금 더 걸리기는 한거 같다.)
그래서, 근래 프로젝트를 진행하면서 사용하게 되어 사용 용례 및 느낀점을 정리하였습니다.
[사용용례]

[느낀점]
OOP적인 느낌(?)과 코드의 확장성을 위해서는 tuple이 편해보인다.
하지만, 로직처리가 많은 경우, 특히 에러코드등의 처리를 위해서는 이전방식(레퍼/포인터)이 더 낳아 보이기도 함.
이부분은 같이 일하는 구성원들과의 합의(?)를 통해 코드 일관성을 유지하는게 좋아 보입니다.
최근에 Javascript, Pyhon 등 다양한 언어 및 32/64bits 환경에서 동시에 작업을 진행하니, 때때로 정리가 않되는 느낌이 있어 정리를 하기위해 기록을 합니다.
기본적으로 32 bits와 64 bits에서의 데이타 사이즈는 아래와 같습니다.

(출처: https://www.ibm.com/docs/en/zos/2.2.0?topic=environments-ilp32-lp64-data-models-data-type-sizes)
하지만, Windows 64bits 환경에서는 차이가 long형의 경우 차이가 있습니다.

(참조: https://docs.microsoft.com/ko-kr/cpp/cpp/fundamental-types-cpp?view=msvc-160)
